Ensemble learning 101
Stacked models, bagging, and boosting
There are a few ideas that describe a situation so well that we cannot help but think that they were tailored for that particular context. However, after researching their origins, we are surprised by the fact that they first emerged long ago and their target application was completely different.
One of such ideas is that of the wisdom of the crowds.
According to its Wikipedia article, “the wisdom of the crowd is the collective opinion of a diverse independent group of individuals rather than that of a single expert” and one of its first appearances dates back to Aristotle, in Politics. Its influences are everywhere: from the structure of juries to the success of social information platforms, such as Reddit.
A surprising twist, though, is that the wisdom of the crowds also seems to have influenced the field of machine learning (ML). In ML, it turns out that if we combine the predictions of multiple independent ML models that, individually, are not that good, we can end up with surprisingly good predictions.
This is the foundational idea behind the technique known as ensembling. Among the notorious ensemble models are random forest and XGBoost, arguably two of the most popular approaches among ML practitioners.
In this post, we first understand when ensembling works. We then explore the three families of techniques that are the most popular in practice: stacked models, bagging, and boosting. Finally, we motivate the need for explainability, which is fundamental in practice but is often neglected with ensembles.
Be the first to know by subscribing to the blog. You will be notified whenever there is a new post.
The need for diversity
We have stated that the idea behind ensembling is similar to that of the wisdom of the crowds: combining the predictions made by many models that, individually, are not that good to end up with great predictions. However, there are two parts of that statement that we have not fully defined yet:
- What does it mean to combine models’ predictions;
- How to pick the models.
The way to combine multiple models’ predictions depends on the type of task. For classification tasks, it often means applying a voting scheme between the models and in the end, outputting the label that the majority of the models predicted. For regression tasks, a common approach is to aggregate the outputs of each model using averages or the median to end up with a single prediction in the end. These are not the only possibilities and, in practice, people often get creative in this stage.

As to the second question, it is clear that we cannot simply use any set of models and expect the combined performance to be drastically improved. Then, what is the necessary condition for the boost in performance to occur?
It turns out that the models need to be diverse. Just like a jury needs people from diverse backgrounds to construct a comprehensive view of the case, we need to ensemble diverse models to improve the overall performance.
If we were to simply combine various similar models, the combined result wouldn’t be much better than the performance of a single model. When we combine diverse models (which mathematically translate to uncorrelated predictors), intuitively, it is as if each model learned different aspects of the data and covered each other’s blind spots, resulting in better predictions overall due to less correlated prediction errors.
Many paths lead to diverse models. That is exactly the difference between each of the three famous families of ensemble methods (stacked models, bagging, and boosting): each one follows a slightly different path toward the goal of finding diverse models.
Stacked models
If we need diverse models, we could simply use different modeling approaches on the same dataset and then combine their predictions.
That’s the path to diversity followed by stacked models.
For example, if we were solving a binary classification problem, we could train a logistic regression, an SVM with a polynomial kernel, and a feedforward neural network, all in the same training set. When it comes time to make predictions, we run the data sample through each model independently and, in the end, predict the label at least two of the models agree on.
As we mentioned, there are many ways to combine the different model’s predictions. Another common approach when it comes to stacked models is to have two layers of models. Layer 0 is comprised of the diverse models (the logistic regression, the SVM, and the neural net, in our example). Layer 1 would be an ML model that learns to predict the correct label based on the outputs of the models in layer 0. By using such an approach, the layer 1 model would be trained to know which layer 0 models are reliable and which are not. The layer 1 model is often referred to as a meta-learner in the literature.
Bagging
Learning different models on the same dataset is not the only way to have a diversity of models. The path to diversity followed by bagging is, instead, using different datasets to train various versions of the same model.
Bagging stands for “bootstrap aggregation”, which perfectly describes the two steps followed by this family of methods.
The first step is the bootstrap. The bootstrap was a statistical breakthrough proposed in the early 1980s. It is much more widely applicable in the field, but the idea in the context of ensembles is to use the bootstrap procedure to construct the different training sets we shall use. This procedure allows us to come up with multiple datasets from a starting point of a single training set.
To do so, for each bootstrapped dataset, we uniformly sample with replacement rows of the original training set. By following this procedure, we arrive at multiple datasets.
The second step is, then, using these bootstrapped datasets to train different versions of the same model and aggregating their outputs to make predictions.

The canonical example of bagging is bagging decision trees. However, the most famous model from the family of bagging is random forests. The foundational idea behind random forests is the same as bagging decision trees. There is, though, an additional catch to ensure even further diversity between each tree.
Random forests provide an improvement over bagged trees by way of a small tweak that decorrelates the trees. (...) when building these decision trees, each time a split in a tree is considered, a random sample of m predictors is chosen as split candidates from the full set of p predictors.
-- Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani. An Introduction to Statistical Learning: with Applications in R. New York. Springer, 2013.
Instead of evaluating the possible splits in every feature, like a regular decision tree, when it comes to finding each split for a tree in the random forest, only a random subset of features is considered. By doing so, the trees learned in each bootstrapped dataset are even more decorrelated, which in turn, results in a boost in the aggregated performance.
Boosting
While bagging achieves diversity by using the bootstrap to arrive at different training sets, boosting follows a distinct approach to diversity.
The idea of boosting is to train many versions of the same model in sequence and, in general, these are very simple models, like stumps. However, each model is trained on a different version of the training set, depending on the performance of the previous model in the sequence.
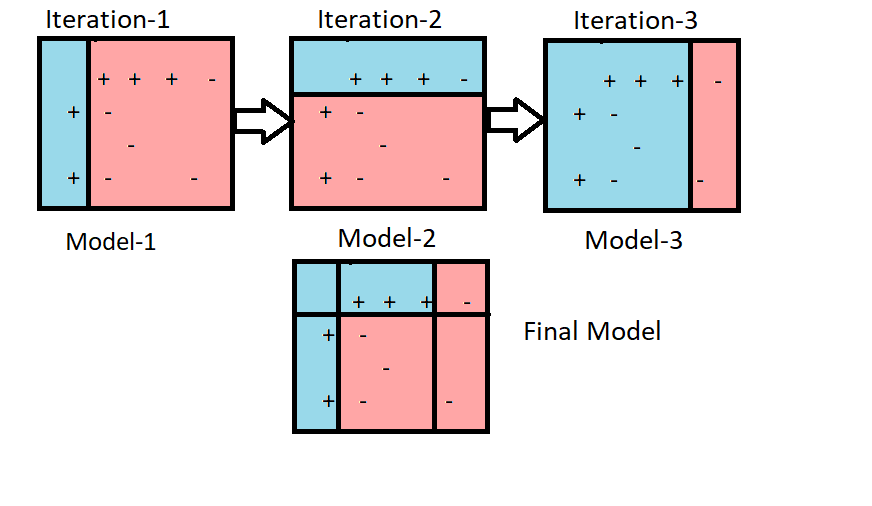
Source: Developing the right intuition for AdaBoost from scratch, Srijani Chaudhury
By following such an approach, each model in the sequence is trained to focus more intensely on the examples that the previous model got wrong. Therefore, as phrased by this blog post, “the second model attempts to correct the predictions of the first model, the third corrects the second model, and so on.”
The gradual focus, in practice, is done by progressively weighting the samples that were mispredicted, which forces the subsequent models to focus more intensely on them.
In the end, to make predictions, all of the models’ predictions are combined, usually weighted according to their performance.
AdaBoost was one of the first notorious algorithms based on the idea of boosting. Another technique based on boosting that repeatedly demonstrates tremendous success, particularly with tabular data, is stochastic gradient boosting, such as XGBoost.
The importance of explainability
Ensembling models, as discussed in this post, often deliver great predictive performance, which justifies their popularity in the industry and in competitions including the famed $1M Netflix Prize.
However, being able to explain the model’s predictions is paramount for trustworthy ML and one of the key differences between the needs for ML in production and ML in academia is the need for explainability. On the trade-off between explainability and predictive performance, ensemble methods often lean towards predictive performance.
Therefore, explainability is often mentioned as one of the drawbacks of using ensembling methods.
One possibility to continue enjoying the predictive performance of ensembles while benefiting from explanations about why the model is behaving a certain way is to use post hoc explanations. SHAP and LIME are two of the most popular explainability techniques, which are both available at Openlayer.
Nowadays, some of the most popular ML approaches in practice are based on ensemble learning, more specifically, on stacked models, bagging, and boosting. These families of methods are linked and their difference lies in how they achieve the required diversity of models that results in the performance boost of ensembles. Understanding the taxonomy of such methods can greatly help practitioners when choosing one approach over the other.
* A previous version of this article listed the company name as Unbox, which has since been rebranded to Openlayer.